Range Sum Query 2D - Immutable

描述

Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.
Figure: The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.

Example:

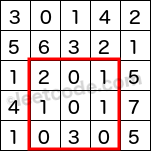
Given matrix =

[
  [3, 0, 1, 4, 2],
  [5, 6, 3, 2, 1],
  [1, 2, 0, 1, 5],
  [4, 1, 0, 1, 7],
  [1, 0, 3, 0, 5]
]

sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12

Note:

  • You may assume that the matrix does not change.
  • There are many calls to sumRegion function.
  • You may assume that row1 ≤ row2 and col1 ≤ col2.

分析

思路跟一维的类似，建立一个累加和矩阵。令状态f[i][j]表示从(0,0)到(i,j)的子矩阵的和，则状态转移方程为

f[i][j] = f[i-1][j] + rowSum

其中 rowSum 是矩阵matrix[i][0]到matrix[i][j]这一行的和。

有了f[i][j]， 则

sumRange(i1,j1,i2,j2) = f[i2][j2] + f[i1-1][j1-1] - f[i1-1][j2]-f[i2][j1-1]

将辅助矩阵f[i][j]的行数和列数增1，可以简化对矩阵边界的处理。

代码

相关题目

results matching ""

    No results matching ""