给定一个无限的整数数据流,如何查询在某个范围内的元素出现的总次数?例如数据库常常需要SELECT count(v) WHERE v >= l AND v < u。这个经典的问题称为范围查询(Range Query)。
方案1: Array of Count-Min Sketches
有一个简单方法,既然Count-Min Sketch可以计算每个元素的频率,那么我们把指定范围内所有元素的sketch加起来,不就是这个范围内元素出现的总数了吗?要注意,由于每个sketch都是近似值,多个近似值相加,误差会被放大,所以这个方法不可行。
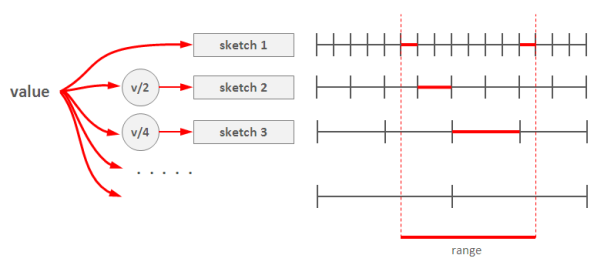
解决的办法就是使用多个“分辨率”不同的Count-Min Sketch。第1个sketch每个格子存放单个元素的频率,第2个sketch每个格子存放2个元素的频率(做法很简答,把该元素的哈希值的最低位bit去掉,即右移一位,等价于除以2,再继续后续流程),第3个sketch每个格子存放4个元素的频率(哈希值右移2位即可),以此类推,最后一个sketch有2个格子,每个格子存放一半元素的频率总数,即第1个格子存放最高bit为0的元素的总次数,第2个格子存放最高bit为1的元素的总次数。Sketch的个数约等于log(不同元素的总数)。
插入元素时,算法伪代码如下,
def insert(x): for i in range(1, d+1): M1[i][h[i](x)] += 1 M2[i][h[i](x)/2] += 1 M3[i][h[i](x)/4] += 1 M4[i][h[i](x)/8] += 1 # ...查询范围[l, u)时,从粗粒度到细粒度,找到多个区间,能够不重不漏完整覆盖区间[l, u),将这些sketch的值加起来,就是该范围内的元素总数。举个例子,给定某个范围,如下图所示,最粗粒度的那个sketch里找不到一个格子,就往细粒度找,最后找到第1个sketch的2个格子,第2个sketch的1个格子和第3个sketch的1个格子,共4个格子,能够不重不漏的覆盖整个范围,把4个红线部分的值加起来就是所求结果